Evaluacija modela (otkrivenog znanja)
Strategije procjene stvarne frekvencije grešaka klasifikacijskog modela
Stvarna frekvencija grešaka klasifikatora je statistički definirana kao frekvencija grešaka ("error rate") na asimptotski velikom broju novih primjera koji konvergiraju stvarnoj populaciji primjera. Empirička frekvencija grešaka se može definirati kao omjer broja pogrešno klasificiranih primjera naspram ukupnom broju klasificiranih primjera.
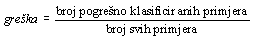
Ukoliko bi imali neograničen primjera, stvarna frekvencija grešaka, mogla bi se izračunati kako se broj primjera približava beskonačnosti.U realnim primjerima, broj primjera je uvijek konačan i relativno malen. Osnovno je pitanje može li se ekstrapolirati empirička frekvencija grešaka izmjerena na konačnom broju primjera na pravu, asimptotsku vrijednost.
Postoji velik broj pristupa za ocjenu stvarne frekvencije grešaka klasifikacijskog modela. Neke od tehnika su bolje od drugih. U statističkom smislu, neke od tih tehnika daju vrijednosti koje su sistematski različite od stvarnih ("biased"); ili su procijenjene frekvencije grešaka sistematski niže od stvarnih ili sistematski više. U nastavku je dan prikaz nekoliko metoda za kvalitetnu procjenu stvarne frekvencije grešaka klasifikatora. Povrh toga razmotreni su faktori koji mogu utjecati na lošu procjenu.
Procjena na osnovu testnog skupa primjera
Kvalitet klasifikatora je odredjen sposobnošću ispravne klasifikacije primjera koji nisu bili uključeni u proces stvaranja modela. Uobičajena je metodologija podjele primjera podataka na dva dijela: skup za učenje ("training set") i skup za testiranje/ocjenu modela ("test set"). Frekvencija grešaka klasifikacijskog modela može se izmjeriti i na skupu za učenje ("training set error rate or reclassification error rate") i na testnom skupu. Prava frekvencija grešaka dobiva se mjerenjem na novim primjerima, a to su u ovom slučaju primjeri iz skupa za testiranje. Slika 1 prikazuje odnos izmedju frekvencije grešaka klasifikacijskog modela na ova dva skupa.

Slika 1: Frekvencija grešaka mjerena na skupu za učenje i prava frekvencija grešaka klasifikacijskog modela, mjerena na skupu novih primjera (test).
Budući da pokušavamo ekstrapolirati našu procjenu rada klasifikacijskog modela mjerenu na konačnom broju primjera, frekvencija grešaka klasifikatora mjerena na skupu primjera za učenje je prva mjera koju možemo koristiti. Kada bismo imali praktički neograničen broj primjera za učenje tada bi i frekvencija grešaka klasifikacijskog modela mjerena na tom uzorku bila vrlo blizu stvarne frekvencije grešaka. No, to nikad nije slučaj u realnim situacijama. U velikom broju slučajeva frekvencija grešaka na skupu za učenje daje vrlo lošu procjenu stvarne vrijednosti klasifikatora. To praktično znači da će u većini situacija stvarna frekvencija grešaka klasifikatora biti znatno veća od one mjerene na skupu primjera za učenje. Razlika izmedju ove dvije mjere je pokazatelj koliko je konkretni klasifikacijski model prekomjerno specijaliziran na karakteristike skupa primjera za učenje ("over-fitted").
Prekomjerna specijalizacija modela ("Over-fitting")
Potpuno je beskorisno generirati klasifikacijski model koji odlično klasificira primjere iz skupa za učenje, a loše klasificira nove primjere. Ovakav problem naziva se prekomjernom specijalizacijom modela ili engl. over-fitting. Stoga je poželjno uvijek koristiti druge mjere za ocjenu kvalitete klasifikacijskog modela.
Budući da u slučaju velikog broja primjera, greška na skupu primjera teži stvarnoj greški modela, može se postaviti pitanje koliko nam je primjera potrebno da bi pouzdano znali stvarnu grešku modela. Postoje i tehnike koje daju vrlo dobru procjenu stvarne greške klasifikacijskog modela, čak i za male skupove podataka (mali broj primjera). Iako ove tehnike daju dobru procjenu stvarne greške modela na skupu primjera za učenje, to ne znači da je stvarna greška klasifikacijskog modela blizu stvarnoj greški za konkretni problem.
Procjena stvarne greške klasifikacijskog modela
Ponekad se greška modela na skupu primjera za učenje koristi kao mjera kvalitete modela, no, to je obično posljedica nepoznavanja pouzdanijih metoda procjene.
Slučajnost - preduvjet za ocjenu stvarne greške modela
Zahtjev koji se postavlja pred bilo koju tehniku procjene stvarne greške modela jest da skup(ovi) primjera koji predstavljaju dio populacije moraju biti slučajno odabrani. To ukratko znači da onaj koji stvara modele ne bi smio utjecati na izbor 'reprezentativnog uzorka' populacije. Koncept slučajnog odabira vrlo je važan kod dobivanja dobre procjene stvarne greške modela. Bez slučajnog odabira, velika je vjerojatnost da će procjena greške biti sistematski kriva, jer će biti izvedena na osnovu uzorka koji loše predstavlja stvarne karakteristike populacije.
Procjena greške metodom 'uči i testiraj', (t&t -"train-and-test")
Kod stvarnih problema, obično imamo uzorak populacije (skup podataka), koji nam je dan na raspolaganje i zadatak da ustanovimo stvarnu grešku modela za populaciju iz koje je potekao dani uzorak. Ovaj tip analize zahtjeva puno manje primjera, jer se podrazumijeva samo jedna polazna populacija primjera, iako nam je ona nepoznata. Štoviše, umjesto korištenja svih primjera radi procjene stvarne greške modela, primjeri se mogu podijeliti u dvije grupe, jedna za generiranje modela, a druga za testiranje modela. Iako ovaj pristup ne daje garancije za dobru procjenu na svim distribucijama primjera, ipak predstavlja procjenu stvarne greške klasifikacijskog modela.
Nije teško vidjeti zašto i za mali skup podataka particioniranje skupa na skup primjera za učenje i skup za testiranje, daje dobre rezultate. Skup primjera za učenje koristi se za stvaranje modela, a testni skup primjer samo za testiranje modela. Ako 'sačuvamo' testni skup primjera nakon što je dizajn modela završen, onda imamo proceduralno identičnu situaciju kao u stvarnosti, t.j. mjerimo grešku modela na novim, nevidjenim primjerima. Ovako odredjenu grešku nazivamo greškom na testnom skupu primjera.
Prirodno, dva skupa primjera morala bi biti slučajni uzorci iste populacije primjera. Osim toga, primjeri iz ta dva skupa trebali bi biti nezavisni. Pod nezavisnošću misli se na da izmedju ova dva skupa ne smije biti bilo kakve veze osim činjenice da potječu iz iste populacije primjera. Postavlja se pitanje: Koliko je primjera potrebno imati u testnom skupu da bi dobili dobru procjenu stvarne greške klasifikacijskog modela.
Odovor je: iznenadjujuče mali broj. Štoviše, na osnovu veličine testnog skupa, znamo koliko velika može biti može biti razlika stvarne greške od one mjerene na testnom skupu. Na slici 3. dan je odnos izmedju procjene greške (t.j. greške na testnom skupu primjera) i moguće najveće stvarne greške u zavisnosti o veličini testnog skupa. Odnos je baziran na vjerojatnosti od 95%, dakle postoji samo 5% vjerojatnost da je odstupanje ve' e od onog prikazanog na grafu. Na primjer, za 50 primjer au testnom skupu, i grešku od 0%, postoji dosta velika vjerojatnost da je stvarna greška i 10%, dok na primjer za testni skup od 1000 primjera stvarna je greška gotovo sigurno ispod 1%. Ovi su rezultati izvedeni iz osnova vjerojatnosne i statističke analize. Bez obzira na stvarnu distribuciju primjera u populaciji, točnost procjene greške klasifikacijskog modela na nezavisnom i slučajno odabranom skupu testnih primjera odredjena je binomnom distribucijom. Dakle, vidimo da je kvaliteta procjene greške na testnom skupu direktno zavisna o broju testnih primjera. Kada testni skup ima 1000 ili više primjera, procjena je vrlo točna. Kod veličine od 5000 primjera procjena na testnom skupu virtuelno je identična stvarnoj greški modela.
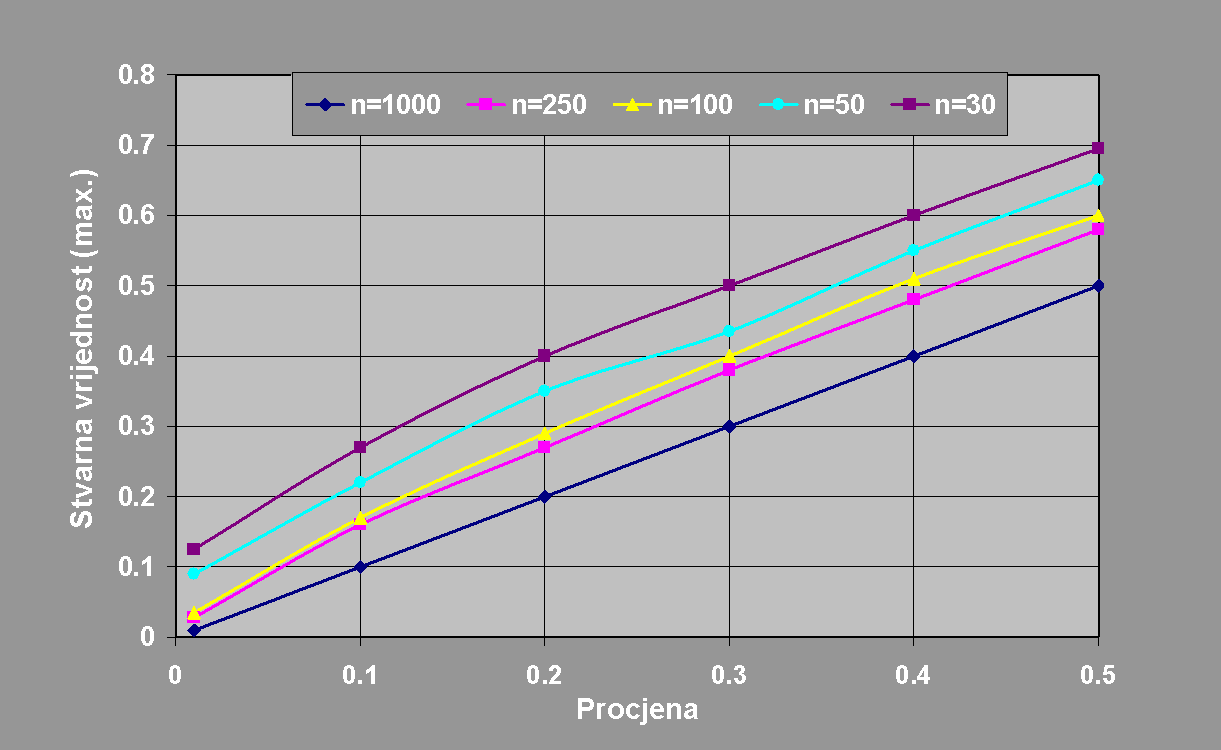
Slika 3: Usporedba procjene greške na testnom skupu sa stvarnom greškom, u zavisnosti o veličini testnog skupa.
Iako je dovoljan broj primjera u testnom skupu ključan za točnost procjene, adekvatan broj primjera u skupu za učenje modela je takodjer ključan. Još jednom je bitno naglasiti važnost slučajnog odabira primjera u ova dva skupa.
Slijedeće logično pitanje jest: koliko primjera izdvojiti u skup za učenje, a koliko u testni skup iz dostupnog skupa podataka? Uobičajen omjer broja primjera u skupu za učenje naspram testnog skupa jest 2/3 naspram 1/3. Jasno je da s premalim brojem primjera u skupu primjera za učenje dizajn klasifikacijskog modela ne može biti kvalitetan, pa je zato veći dio primjera u skupu za učenje modela.
Metode višestruke unakrsne validacije ("resampling"), ili višestruke t&t metode, daju bolju procjenu stvarne greške modela. Te su metode ustvari varijacija osnovne t&t metode i biti će objašnjene u slijedećem poglavlju.
© 2001 LIS - Institut Rudjer Bošković
Posljednja izmjena: September 08 2015 09:28:57.