DMS Tutorial - Neural networks

Neuralne mreže

Neuralne mreže ili umjetne neuralne mreže, predstavljaju gusto isprepletene mreže medjusobno povezanih računskih elemenata. Osnovni element takve mreže jest neuron, prikazan na slici 1.

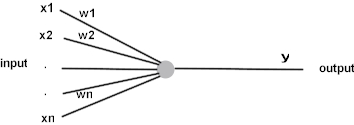
Slika 1: Neuron, osnovni računski element neuronsle mreže

Ulazni dio neurona čini skup vrijednosti x1,x2, ...,xn, a izlazni vrijednost y. I ulazne i izlazna vrijednost neurona poprimaju kontinuirane (realne) numeričke vrijednosti, tipično iz intervala (0,1). Neuron izračunava težinski zbroj ulaznih vrijednosti, koristeći posebnu vrijednost 'praga' ("threshold"), T, kroz poseban funkcionalni izraz (sigmoidalna funkcija):

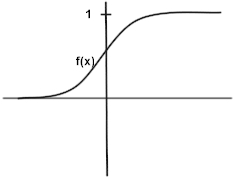
Slika 2: Sigmoidalna funkcija

Dakle, svaki element neuralne mreže, neuron, izračunava svoju izlaznu vrijednost prema slijedećem izrazu:

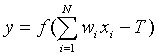
gdje w_i predstavljaju težinske faktore veza izmedju neurona. Izlazne vrijednosti pojedinih neurona predstavljaju ulazne vrijednosti drugih neurona. U topologijitzv. više-slojnog perceptrona (postoji mnogo različitih topologija neuralnih mreža od kojih je više-slojni preceptron najpoznatija), neuroni su grupirani u slojeve kao što je prikazano na Slici 3. Izlazne vrijednosti jednog sloja čvorova u mreži predstavljaju ulazne vrijednosti slijedećeg sloja u mreži perceptrona. Ulazne vrijednosti prvog sloja (ulazni sloj) su ustvari ulazne vrijednosti u mrežu, dok izlazne vrijednosti zadnjeg sloja predstavljaju i izlazne vrijednosti mreže. Više-slojni perceptron je posebno pogodan za aproksimiranje klasifikacijskih funkcija, koje preslikavaju odredjeni vektor numeričkih vrijednosti (x₁,x₂, ... x_n) u jednu ili više klasa C₁,C₂,...C_m. Uz unaprijed zadanu strukturu mreže (slojevi, čvorovi i grane), konačni oblik (model) neuralne mreže odredjuje se optimiranjem težinskih faktora w_i grana mreže i vrijednosti praga T, svakog od čvorova. Optimizacija težinskih faktora provodi se metodom učenja ("supervised learning") na osnovi velikog broja primjera. Primjeri iz skupa podataka za učenje se koriste jedan po jedan, te se za svaki primjer izračunavaju izlazne vrijednosti mreže i usporedjuju sa željenom izlaznom vrijednosti. Potom se težinski faktori i vrijednosti 'praga' mijenjaju proporcionalno veličini greške koju su uzrokovali u izlaznoj vrijednosti. Jedna od prvih i najčešće korištenih metoda optimiranja mrežnih parametara jest metoda 'propagacije greške-unatrag' ("back-propagation"), kojom se na iterativan način 'šire' greške na unutarnje slojeve mreže, i tu koriste za korigiranje (optimizaciju) težinskih faktora grana mreže.

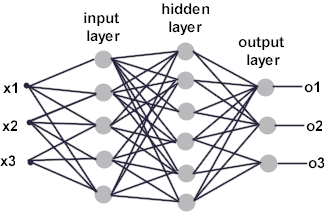
Slika 3: Više-slojni perceptron

Kada primijenjivati neuralne mreže?

Neuralne mreže vrlo se dobro ponašaju upravo na težim klasifikacijskim problemima, kod kkojih je teško ili nemoguće koristiti druge metode, poput stabla odlučivanja ili metoda indukcije, koje 'presijecaju' prostor primjera linearnim funkcijama (obično paralelno na osi atributa).
Jedan od nedostataka neuralnih mreža jest relativno spor i zahtjevan proces 'učenja' modela (optimizacije težinskih faktora), nasuprot jednostavnijim metodama (odnos prema metodama poput stabla odlučivanja je i do 2 do 3 reda veličine!). Pored toga treba imati na umu da neuralne mreže ne nude kao konačni model podataka razumljiv odnos važnih varijabli. Umjesto toga model, dakle neuralna mreža, jest implicitan, t.j. odnosi izmedju varijabli skriveni su u mrežnoj strukturi i težinskim faktorima veza neuralne mreže.

WWW tekstovi o neuralnim mrežama

An introduction to neural networks
by A. Blais and D. Mertz
http://www-106.ibm.com/developerworks/linux/library/l-neural/?open&l=805,t=grl,p=NeuralNets

Neural networks
by C. Stergiou and D. Siganos
http://www.doc.ic.ac.uk/~nd/surprise_96/journal/vol4/cs11/report.html

Neural nets overview
by J. Fröhlich
http://rfhs8012.fh-regensburg.de/~saj39122/jfroehl/diplom/e-13.html

Mini-tutorial on artificial neural networks
by S. L. Thaler
http://www.imagination-engines.com/ann.htm

Artificial neural networks
by F. Rodriguez
http://www.gc.ssr.upm.es/inves/neural/ann1/anntutorial.html