DMS Pregled područja - Stabla odlučivanja

Stabla odlučivanja

Stabla odlučivanja vrlo su moćne i popularne tehnike modeliranja za klasifikacijske i predikcijske probleme. Privlačnost stabla odlučivanja leži u činjenici da, u odnosu na npr. neuralne mreže nude modela podataka u 'čitljivom', razumljivom obliku - ustvari u obliku pravila. Ta pravila se lako mogu direktno interpretirati običnim jezikom, ili pak koristiti u nekom od jezika za rad s bazama podataka (SQL), tako da se odredjeni primjeri iz baze mogu izdvojiti korištenjem pravila generiranih stablom odlučivanja.

Za neke je probleme od ključne važnosti samo točnost klasifikacije ili predikcije modela. U takvim slučajevima čitljivost modela nije od presudne važnosti. No, u drugim situacijama upravo sposobnost interpretiranja modela 'ljudskim' jezikom je od ključne važnosti. U marketingu potrebno je npr. dobro opisati različite segmente populacije kupaca za marketinške stručnjake kako bi oni mogli organizirati efektivnu kampanju radi povećanja prometa odredjenih proizvoda. Dakle, generirani modeli moraju biti čitljivi za eksperte iz domene problema i oni moraju prepoznati i odobriti primjenu znanja sadržanog u novim modelima. Postoji čitav niz različitih algoritama za konstruiranje stabla odlučivanja koji nude imaju ove osnovne kvalitete ove tehnike. Najpoznatiji i vjerojatno najviše korišten algoritam stabla odlučivanja jest C4.5 (odnosno njegova poboljšana iako komercijalne verzija See5/C5.0).

Što je stablo odlučivanja ?

Stablo odlučivanja jest klasifikacijski algoritam u formi stablaste strukture (Slika 1), u kojoj se razlikuju dva tipa čvorova povezanih granama:

a krajnji čvor ("leaf node") - kojim završava odredjena grana stabla. Krajnji čvorovi definiraju klasu kojoj pripadaju primjeri koji zadovoljavaju uvjete na toj grani stabla;
a čvor odluke ("decision node") - ovaj čvor definira odredjeni uvjet u obliku vrijednosti odredjenog atributa (varijable), iz kojeg izlaze grane koje zadovoljavaju odredjene vrijednosti tog atributa.

Stablo odlučivanja može se koristiti za klasifikaciju primjera, tako da se krene od prvog čvora odlučivanja u korijenu stabla i kreće po onim granama stabla koja primjer sa svojim vrijednostima zadovoljava sve do krajnjeg čvora koji klasificira primjer u jednu od postojećih klasa problema.

Osnovni preduvjeti za korištenje tehnike stabla odlučivanja su:

Opis u obliku parova vrijednosti-atributa - podaci o primjeru moraju biti opisani u obliku konačnog broja atributa;
Prethodno definiran konačan broj klasa (vrijednosti ciljnog atributa) - kategorije kojima primjeri pripadaju moraju biti definirane unaprijed i treba ih biti konačan broj;
Klase moraju biti diskretne - svaki primjer mora pripadati samo jednoj od postojećih klasa, kojih mora biti znatno manje negoli broja primjera;
Značajan broj primjera - obično je poželjno da u skupu primjera za generiranje stabla odlučivanja postoji barem nekoliko stotina primjera.

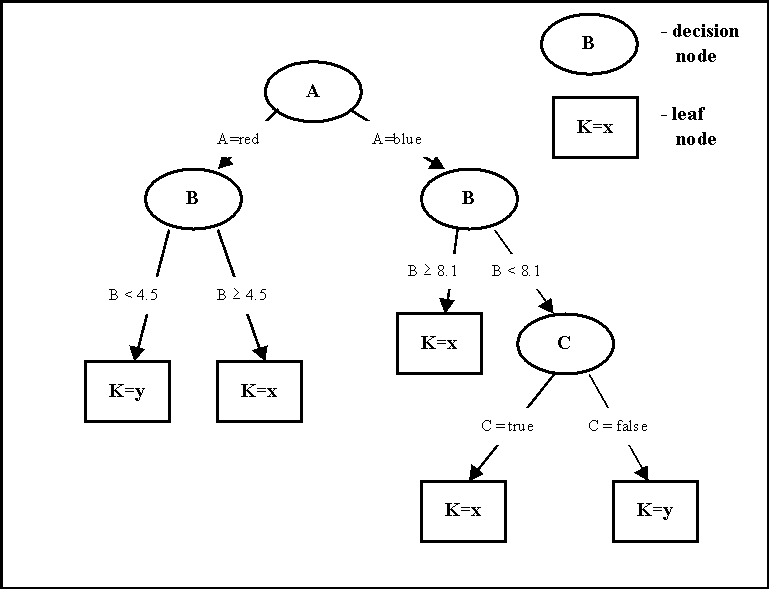
Slika 1: Primjer jednostavnog stabla odlučivanja

Proces stvaranja stabla odlučivanja

Većina postojećih algoritama stabla odlučivanja su varijacije osnovnog algoritma koji posjeduje jednostavne karakteristike "greedy", "top-down" metode pretraživanja prostora rješenja.

J. Ross Quinlan razvio je svoj ID3 algoritam još prije dobrih tridesetak godina i prikazao ga u svojoj knjizi iz 1975. godine (Machine Learning, vol. 1). ID3 algoritam baziran je na tzv. Concept Learning System (CLS) algoritmu, i prikazan je na Slici 2.

_______________________________________________________
 funkcija ID3
 Input:   (R: skup nezavisnih atributa,
 C: ciljni(zavisni) atribut,
 S: skup primjera za učenje)
 kao rezultat daje stablo odlučivanja;
 počni
 
 Ako je  S prazan, napravi jedan čvor s vrijednošču
 Pogrešno;
 Ako se S sastoji od primjera s istom vrijednošću ciljnog
 atributa, napravi jedan krajnji čvor s tom vrijednosti
 ciljnog atributa;
 Ako je R prazan, tada napravi jedan (krajnji) čvor s vrijednosti
 koja je najčešća za ciljni atribut za skup S; (u tom
 slučaju stablo će vjerojatno raditi i pogrešne klasifikacije
 na skupu S, u mjeri u kojoj su zastupljeni primjeri ostalih klasa);
 Neka je A atribut s najvećom vrijednosti Gain(A,S) izmedju
 svih atributa u R;
 Neka su {aj| j=1,2, .., m} vrijednosti atributa A;
 Neka su {Sj| j=1,2, .., m} podskupovi S koji se sastoje
 od primjera koji imaju aj za atribut A;
 Napravi stablo s korijenom označenim A, te granama
 a1, a2, ..., am koja vode na stabla
 (ID3(R-{A}, C, S1), ID3(R-{A}, C, S2),
 .....,ID3(R-{A}, C, Sm);
 Rekurzivno primjeni ID3 to na podskupove {Sj| j=1,2, .., m}
 sve dok oni nisu prazni;
 kraj
 _______________________________________________________

Slika 2: ID3 algoritam

ID3 pretražuje preko atributa svih primjera u skupu podataka, te nalazi atribut koji najbolje odvaja primjere odredjene klase. Ukoliko atribut savršeno razdvaja klase ID3 algoritam se zaustavlja; inače se rekurzivno izvršava na m podskupova (gdje m označava broj mogućih vrijednosti atributa), tražeći 'najbolje' atribute za njihovo razdvajanje. Algoritam koristi "greedy" pristup, t.j. traži trenutno najbolji atribut i nikad ne 'gleda' unatrag, da bi provjerio ispravnost prethodnih izbora, odnosno razdvajanja. Treba imati na umu da ID3 može generirai stabla koja rade i pogrešne klasifikacije na skupu primjera za učenje.

Centralni dio algoritma jest selekcija atributa za stvaranje čvora odlučivanja, t.j. atributa koji će poslužiti za razdvajanje odredjene grane stabla. Za selekciju atributa sa najheterogenijom strukturom vrijednosti ciljnog atributa, algoritam koristi koncept entropije, koji je podrobnije objašnjen u daljnjem tekstu.

Koji je atribut najbolji klasifikator?

Kriterij kvalitete u algoritmu stabla odlučivanja vezan je uz selekciju atributa koji će poslužiti kao kriterij za razdvajanje primjera u odredjenom čvoru odlučivanja stabla. Cilj je odabrati atribut koji je najupotrebljiviji s obzirom na osnovni cilj, klasifikaciju primjera. Dobra kvantitativna mjera vrijednosti atributa u tom smislu je statistička vrijednost nazvana informacisjki dobitak ("information gain"), kojom se mjeri kako dobro dani atribut razdvaja primjere prema njihovoj klasifikaciji. Ova se mjera koristi da bi se odabrao najbolji kandidat (atribut) u svakom novom koraku stvaranja stabla odlučivanja.

Entropija - mjera homogenosti skupa primjera

Da bi precizno definirali informacijski dobitak, potrebno je definirati mjeru, koja se često koristi u teoriji informacija, a naziva se entropija. Entropija karakterizira 'čistoću nekog skupa primjera. Uz zadan skup S, koji u ovom primjeru, jednostavnosti radi, sadrži samo dvije klase, pozitivne i negativne primjere, entropija ove binarne klasifikacije je definirana slijedećim izrazom:

Entropija(S) = - p_plog₂ p_p p_nlog₂ p_n

gdje p_p označava proporciju (postotak) pozitivnih primjera u S, a p_n proporciju negativnih primjera u skupu S. U svim proračunima entropije pretpostavlja se da vrijedi 0log0=0.

Da bi bolje ilustrirali, pretpostavimo da je S skup od 25 primjera, 15 pozitivnih i 10 negativnih,[15+,10-]. Tada je entropija u odnosu na ovu klasifikaciju:

Entropija(S) = - (15/25) log₂ (15/25) - (10/25) log₂ (10/25) = 0.970

Treba primijetiti da je entropija 0, ako svi članovi skupa S pripadaju istoj klasi primjera. Npr., ako su svi primjeri pozitivni, tada vrijedi p_p= 1, odnosno p_n= 0, te je zato Entropija(S) = -1´ log₂(1) - 0´ log₂0 = -1´ 0 - 0´ log₂0 = 0. Isto tako entropija je maksimalna (1) ukoliko skup S sadrži istovjetan broj pozitivnih i negativnih primjera. Ako skup S sadrži nejednak broj pozitivnih i negativnih primjera, entropija poprima vrijednost iz intervala 0 i 1. Slika 3 prikazuje oblik entropije u odnosu za binarnu klasifikaciju, u ovisnosti o proporciji pozitivnih primjera u skupu S (p₊ varira izmedju 0 i 1).

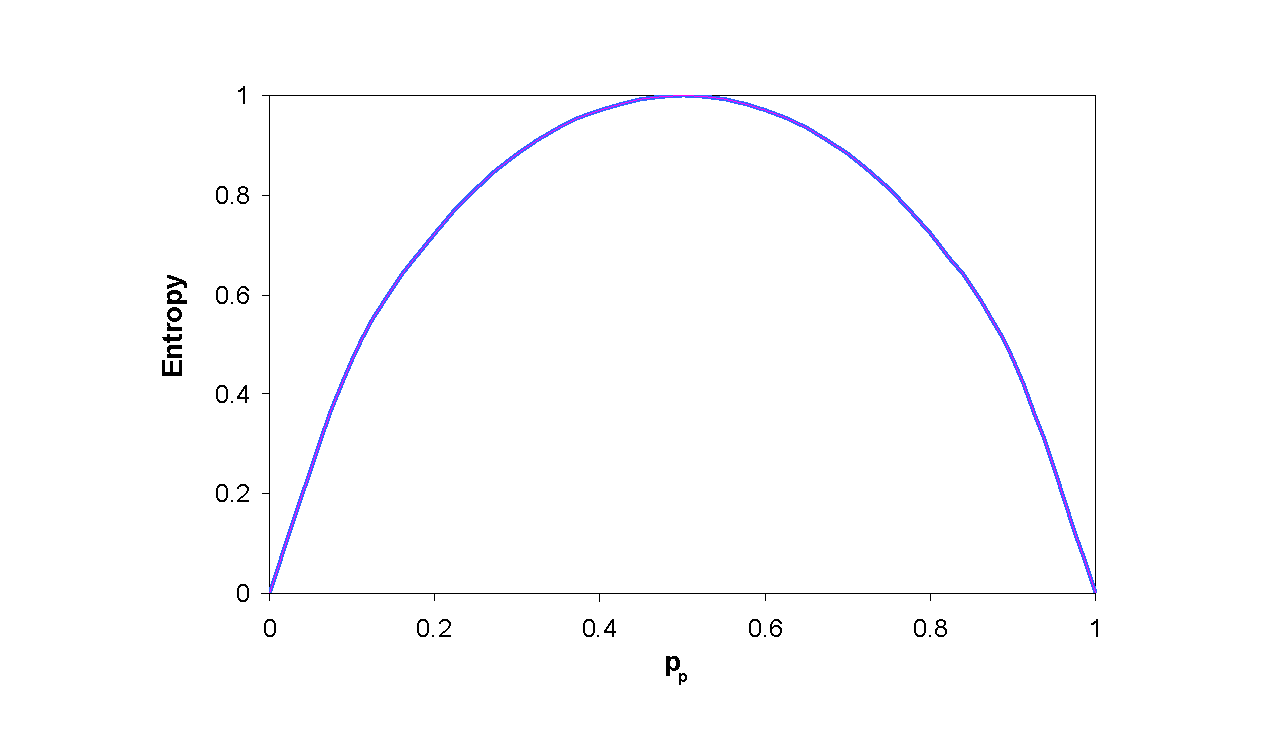
Slika 3: Entropija u slučaju binarnog klasifikacijskog problema, u ovisnosti o proporciji pozitivnih primjera u skupu S (p₊varira izmedju 0 i 1).

Jedna od interpretacija entropije iz teorije informacija jest da ona specificira minimalni broj bitova informacije potreban da se kodira klasifikacija bilo koje člana skupa S (t.j. ako se primjer iz skupa S slučajno odabere). Npr. ukoliko je p_p 1, tada primatelj informacije zna da će (svaki) primjer biti pozitivan, pa prema tome nije potrebna nikakva poruka i entropija je 0. Nasuprot tome ako je p_p=0.5, jedan bit je potreban da bi se znalo da li je primjer pozitivan ili negativan. Ako je pak p_p=0.8, tada je potreban skup poruka duljine u prosjeku manje od 1 bita i to kraće za pozitivne primjere i dulje za negativne.

Ukoliko ciljni atribut poprima više od dvije vrijednosti, npr. c različitih vrijednosti, tada je entropija skupa S u odnosu na takvu klasifikaciju definirana sa:

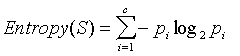
gdje je p_i proporcija klase i u skupu S. Treba primijetiti da ako ciljni atribut poprima c različitih vrijednosti maksimalna entropija iznosi log₂c.

Informacijski dobitak mjeri očekivanu redukciju entropije

Uz danu entropiju kao mjeru 'nečistoće' u skupu primjera, sada možemo definirati mjeru efektivnosti atributa u klasificiranju primjera. Ta mjera, informacijski dobitak, predstavlja očekivanu redukciju entropije uzrokovanu razdvajanjem primjera na osnovu tog atributa. Točnije, informacijski dobitak, Gain (S,A), atributa A, u odnosu na skup primjera S, definiran je kao:

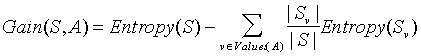
gdje je Values(A)skup svih mogućih vrijednosti atributa A, a S_v podskup od S, za koji atribut A ima vrijednost v (t.j., S_v = {s Î S | A(s) = v}). Prvi član u jednadžbi za Gain je entropija originalnog skupa S dok je drugi član očekivana vrijednost entropije nakon što je S razdvojen korištenjem atributa A. Očekivana entropija opisana drugim članom jednostavno je zbroj entropija podskupova S_v, s težinom proporcionalnom dijelu primjera |S_v|/|S| koji pripadaju S_v. Gain (S,A) je dakle očekivana redukcija entropije uzrokovana poznavanjem vrijednosti atributa A. Ili, na drugi način, Gain(S,A) je informacija o vrijednosti ciljnog atributa, uz poznate vrijednosti atributa A.

Proces odabira novog atributa i razdvajanja primjera, ponavlja se za svaki čvor odlučivanja, uz to da se koriste samo oni primjeri koji pripadaju tom čvoru. Pri tom su svi atributi korišteni prije tog čvora a u istoj grani stabla, isključeni iz daljnjeg odabira, što znači da se mogu pojaviti samo jednom na odredjenoj grani stabla. Ovaj se proces nastavlja sve dok na odredjenom čvoru nije zadovolojen jedan od dva kriterija:

svi atributi su već bili korišteni u toj grani stabla, ili
svi primjeri koji pripadaju tom čvoru imaju istu klasu - prema tome radi se o krajnjem čvoru grane (entropija primjera jednaka je nuli).

Problemi u modeliranju podataka metodom stabla odlučivanja

Praktična strana primjene metode stabla odlučivanja uključuje rješavanje problema poputnivoa kompleksnosti stabla, tretman kontinuiranih (numeričkih) atributa, tretman atributa s neodredjenim vrijednostima, poboljšanja efikasnosti algoritma. U daljnjem tekstu podrobnije ćemo se pozabaviti ovim problemima.

Izbjegavanje "over-fitting"-a podataka

U principu algoritam na slici 2 može generirati stablo, dovoljno kompleksno da točno klasificira sve primjere iz skupa podataka za učenje. Iako je to u odredjenim slučajevima razumna strategija, u većini situacija to radja dodatne probleme, bilo zbog 'šuma u podacima, ili pak nedovoljno velikog uzorka podataka koji bi trebao reprezentirati populaciju primjera za odredjeni klasifikacijski problem. Bez obzira da li se radi o prvom ili drugom slučaju, jednostavni algoritam prikazan na Slici 2, bi generirao stablo koje 'pretjerano dobro' ("over-fitting") aproksimira odnose u podacima.

"Over-fitting" je značajna poteškoća u primjeni metoda stabla odlučivanja, ali i drugih tehnika modeliranja podataka. Nekoliko je mogućih rješenja za izbjegavanje "over-fitting"-a.Ona se mogu grupirati na slijedeći način:

rješenja koja zaustavljaju proces rasta stabla prije nego se postigne savršena klasifikacija primjera iz skupa podataka za učenje;
rješenja u kojima se najprije generira stablo koje savršeno klasificira primjere, a potom se odredjene grane stabla 'skraćuju' prema prethodno definiranom kriteriju.

Iako se na prvi pogled prvi pristup čini direktnijim, drugi se pristup u praksi pokazao pouzdanijim. To je posljedica toga što je teško unaprijed definirati željenu kompleksnost stabla odlučivanja.

Bez obzira na odabrani pristup, glavno je pitanje kako ćemo odrediti optimalnu kompleksnost, odnosno veličinu stabla za konkretni problem. Kao rješenja nameću se slijedeći pristupi:

Korištenje posebnog skupa primjera (validacijski skup), koji je različit od onog korištenog za generiranje stabla, da bi se ocijenila uspješnost 'skraćivanja' stabla;
Korištenje posebnog statističkog testa na čvorovim koji su kandidati za 'skraćivanje', kojima se pokazuje da li će se izbacivanjem tog čvora postići poboljšanje;
Korištenje eksplicitne mjere kompleksnosti kodiranja primjera stablom odlučivanja, koja zaustavlja rast stabla kada je taj kriterij zadovoljen. Ovaj pristup baziran je na heuristiv kom principu koji se naziva "Minimum Description Length".

Prvi od ovih pristupa je i najčešći. Kod ovog pristupa, primjeri se dijele u dva skupa: skup za učenje ("training set") koji se koristi za generiranje stabla, te skup za provjeru ("validation set"), koji se koristi za provjeru učinkovitosti metode skraćivanja stabla.

Problem numeriv kih atributa

Osnovni oblik ID3 algoritma ograničen je na atribute koji imaju ograničen skup diskretnih vrijednosti. Kao prvo ciljni atribut mora imati ograničen broj kategorija (klasa). Nadalje, atributi koji se testiraju u čvorovima odlučivanja takodjer moraju imati diskretne vrijednosti. Ovaj drugi zahtjev se može relativno lako zadovoljiti i u slučaju da je atribut numeričkog tipa (realne numeričke varijable). To se može postići dinamičkim definiranjem novih diskretnih vrijednosti realnih varijabli koje dijele vrijednosti tog atributa u diskretni skup intervala. Konkretno za atribut A koji je numeriv kog tipa, možemo primijeniti algoritam koji će dinamički kreirati novi atribut binarnog tipa A_c koji poprima vrijednost 1 ("true") ako vrijedi A < c odnosno 0 ("false") ako prethodna tvrdnja nije točna. Pitanje je kako doći do granica interesantnih intervala, t.j. vrijednosti c. Naravno, mi bismo željeli vrijednosti c, koje će nam dati najveći informacijski dobitak ("Gain"). Sortiranjem primjera prema vrijednostima atributa A, te identificiranjem susjednih primjera koji pripadaju različitim klasama ciljnog atributa možemo generirati skup vrijednosti c u sredini intervala vrijednosti atributa A za takva dva susjedna primjera. Može se pokazati da vrijednosti c koje maksimiziraju informativni dobitak uvijek leže na ovako definiranim granicama intervala. Ovako definirane diskretne vrijednosti atributa mogu poslužiti za izračunavanje informacijskog dobitka koji im pripada, i tako učestvovati u procesu selekcije sa ostalim atributima koji su na raspolaganju za generiranje stabla.

Problem atributa s neodredjenim vrijednostimai ("missing values")

U mnogim praktičnim primjenama postoje atributi kod kojih odredjeni postotak primjera ima neodredjene vrijednosti ("missing values"). Na primjer, u medicinskoj domeni čest je slučaj da su odredjeni rezultati laboratorijskih testova dostupni samo za dio pacijenata. U tom je slučaju uobičajeno da se vrijednosti tih atributa (testova) odrede na osnovu ostalih primjera (pacijenata) koji posjeduju rezultate tih testova.

Razmotrimo situaciju u kojoj treba izračunati Gain(S, A) za čvor n u stablu, za atribut A da bi odredili da li taj atribut predstavlja kandidata za test na čvoru n. Pretpostavimo da je <x, c(x)> jedan od primjera iz skupa za učenje S te da je vrijednost A(x) nepoznata, gdje c(x) predstavlja vrijednost ciljnog atributa (klasu) primjera x.

Jedna od strategija za rješavanje ovog problema bila bi da se umjesto neodredjene vrijednosti za atribut A koristi najčešća vrijednost za taj atribut, u primjerima koji se nalaze na čvoru n. Kao druga mogućnost pojavljuje se nadomještanje s najčešćom vrijednosti tog atributa kod primjera iste klase c(x), na čvoru n.

Prednosti i slabe strane metode stabla odluv ivanja

Prednosti metode stabla odlučivanja su:

Sposobnost generiranja razumljivih modela;
Relativno mali zahtjevi na računalne resurse (vrijeme i memorija);
Sposobnost korištenja svih tipova atributa (kategorički, numerički);
Stabla odlučivanja jasno odražavaju važnost pojedinih atributa za konkretni klasifikacijski odnosno predikcijski problem.

Slabe strane metode stabla odlučivanja

Metode stabla odlučivanja su manje prikladne za probleme kod kojih se traži predikcija kontinuiranih vrijednosti ciljnog atributa;
Metode Stabla odlučivanja sklona su greškama u više-klasnim problemima sa relativno malim brojem primjera za učenje modela;
U nekim situacijama generiranje stabla odlučivanja može bit računalno zahtjevan problem. Sortiranje kandidata za testiranje na čvorovima stabla može biti zahtjevno, kao i metode 'skraćivanja' stabla, kod kojih je često potrebno generirati velik broj stabala da bi odabrali ono koje je najbolje za klasifikaciju primjera odredjenog problema;
Stabla odlučivanja nisu dobro rješenje za klasifikacijske probleme kod kojih su regije odredjenih klasa 'omedjene' nelinearnim krivuljama u više-dimenzionalnom atributnom prostoru. Većina metoda stabla odlučivanja testiraju u svojim čvorovima vrijednosti jednog atributa, i time formiraju pravokutne regije i više-dimenzionalnom prostoru;

WWW tekstovi o metodi stabla odlučivanja

Overview of Decision Trees
by H.Hamilton. E. Gurak, L. Findlater W. Olive
http://www.cs.uregina.ca/~dbd/cs831/notes/ml/dtrees/4_dtrees1.html