DMS Pregled područja - asocijativna pravila

Asocijativna pravila

Asocijativna pravila koriste se prije svega u obradi podataka u obliku transakcija. Važni termini u terminologiji asocijativnih pravila su:

Element ili dio (u terminologiji obrade podataka uobičajenije je korištenje par atribut-vrijednost);

Transakcija (skup elemenata, korespondira terminu primjer u području obrade podataka);

Skup transakcija (korespondira pojmu skupa podataka).

Tipično za transakcije je da se razlikuju u broju elemenata, što uglavnom inače nije slučaj s podacima koji se pripremaju za obradu podataka nekom od metoda modeliranja. Stoga je za većinu ostalih metoda modeliranja podataka nužno transformirati transakcijske podatke.

Svaka transakcija u skupu transakcija, daje nam informaciju o tome koji elementi se zajedno pojavljuju u transakcijama. Korištenjem transakcija moguće je napraviti tablice koje nam daju frekvenciju pojavljivanja parova (ili većeg broja elemenata) odredjenih elemenata u transakcijama. Iz tih tablica lako je napraviti jednostavna pravila poput:

R₁="Element 1 pojavljuje se zajedno s elementom 2 u 10 vih transakcija"

10% je mjera frekvencije pojavljivanja para elemenata 1 i 2 u skupu svih transakcija i predstavlja 'značaj' ili 'signifikantnost' pravila ("support"). Ako je frekvencija pojavljivanja elementa 1 u svim transakcijama 15%, a elementa 2, 20%, tada omjer broja transakcija u kojima se pojavljuju oba elementa (odnosno značaj pravila) prema broju transakcija u kojima se pojavljuje element 1 (uvjetni dio pravila), nazivamo pouzdanošću ("confidence") pravila. U ovom je slučaju pouzdanost pravila R₁:

c (R₁) = 10/15 = 0.666

Lako je napraviti i inverzno pravilo:

R₂="Element 2 pojavljuje se zajedno s elementom 1 u 10 vih transakcija"

Iako se naizgled radi o istom pravilu, svojstva R₁i R₂ se razlikuju. Tako je pouzdanost pravila:

c (R₂) = 10/20 = 0.500

Što nam pouzdanost pravila govori? Pouzdanost pravila od 0.5 jednaka je tvrdnji da kada se u transkaciji pojavi element 2, postoji 50% vjerojatnost da će se u istoj transakciji pojaviti takodjer i element 1. Na prvi pogled izgleda da su najpouzdanija pravila ona koja su najbolja. No, problem je kada se npr. element 1 pojavljuje vrlo često u transakcijama. (recimo, u 60% transakcija). U tom slučaju pravilo može imati slabiju pouzdanost od sasvim slučajnog odabira! To pokazuje da nam kao mjera dobrog pravila treba nešto bolje od pouzdanosti. Ta mjera naziva se poboljšanjem ("improvement"). Ta nam mjera govori o tome koliko je odredjeno pravilo bolje od slučajnog odabira. Poboljšanje je dano slijedećim izrazom:

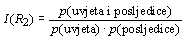
U našem slučaju I(R₂)=0.2/(0.2*0.1)=10, dok je za pravilo R₁, I(R₁)=0.1/(0.1*0.2)=5. Kada je poboljšanje veće od 1, pravilo je bolje od slučajnog odabira, kada je manje od 1, onda je gore. U našem je slučaju R₂ 10 puta, a R₁ 5 puta bolje od slučajnog odabira.

Generiranje asocijativnih pravila je iterativni proces. U svojoj biti vrlo je jednostavan i svodi se na jednostavnu shemu:

generiraj tablicu frekvencija pojavljivanja pojedinačnih elemenata;
generiraj tablicu frekvencija pojavljivanja dva različita elementa. Iz tablice izdvoji parove s poboljšanjem većim od unaprijed zadanog kriterija;
generiraj tablicu frekvencija pojavljivanja tri različita elementa. Iz tablice izdvoji 'triplete' s poboljšanjem većim od unaprijed zadanog kriterija;
.........

Primjena asocijativnih pravila

Asocijativna pravila koriste se u analizi tzv. 'potrošačkih košarica' ("market basket analysis"), primarno zbog jasnoće i iskoristivosti dobivenih pravila. Ona jasno izražavaju u kojoj su mjeri važni produkti korelirani, te time sugeriraju konkretne akcije. Asocijativna pravila koriste se prije svega u obradi podataka kod kojih su atributi nominalnog (kategoričkog) tipa. Osim samog procesa generiranja asocijativnih pravila, za proces primjene ove tehnike važno je efikasno riješiti i slijedeće probleme:

Izbor pogodnog skupa elemenata

Osnova za obradu podataka metodom asocijativnih pravila su obično detaljni podaci skupljeni na licu mjesta - točki prodaje artikala, npr. No, to ne znači da ćemo konkretne produkte u tim transakcijama automatski proglasiti elementima (primjerima) za proces obrade. Obično su artikli u prodavaonicama svrstani u kategorije (taksonomija). Izbor pravog nivoa kategorizacije može igrati ključnu ulogu u smislenosti konačnih pravila, ali i redukciji velikog broja artikala u jedan element. Desetci, ponekad i stotine artikala mogu biti svedeni na jednu ili više kategorija (elemenata), koji dobro reprezentiraju generalna svojstva svih artikala koje prodaje odredjeni odjel.

Praktična ograničenja - velik broj elemenata koji se pojavljuju u velikom broju interesantnih pravila

Broj kombinacija za skupove s više elemenata ("itemsets") raste eksponencijalno s brojem elemenata u transakcijama. Broj potrebnih izračuna mjera (značaj, pouzdanost, poboljšanje) skupova elemenata, za npr., velik trgovački centar s tisućama različitih artikala, brzo raste preko milion, kako raste i broj mogućih elemenata u skupovima. Npr. za 1000 različitih produkata, ukupan broj mogućih skupova od tri elementa jest:

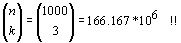
Kao što se iz ovog može naslutiti, izračunavanje frekvencija i mjera kvalitete za skupove elemenata s pet ili više elemenata vrlo lako može biti potpuno besmisleno (vremenski neizvedivo). U tom je slučaju od prvorazrednog značaja prethodno spomenuto korištenje taksonomija, odnosno generalizacija elemenata.

Jake strane metode asocijativnih pravila su slijedeće:

asocijativna pravila su jednostavna i jasna;

metoda je namijenjena problemima koji nisu klasifikacijskog odnosno prediktivnog tipa, t.j. nema ciljnog atributa;

omogućuje obradu podataka kod kojih primjeri imaju varijablini broj atributa;

algoritmi kojima se generiraju asocijativna pravila u principu su vrlo jednostavni.

WWW tekstovi o metodi asocijativnih pravila

Tutorial on High Performance Data Mining
by Vipin Kumar and Mahesh Joshi
http://www-users.cs.umn.edu/~mjoshi/hpdmtut.ppt

ARMiner - a client-server data mining application specialized in finding association rules
maintained by L.Cristofor.
http://www.cs.umb.edu/~laur/ARMiner/